A. Pengertian segitiga
Perhatikan sisi-sisinya, ada berapa sisi-sisi yang
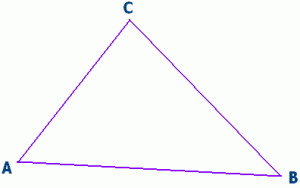
membentuk segitiga ABC? Sisi-sisi yang membentuk segitiga ABC
berturut-turut adalah AB, BC, dan AC. Sudut-sudut yang terdapat pada segitiga ABC sebagai berikut.
a. sudut A atau sudut BAC atau sudut CAB.
b. sudut B atau sudut ABC atau sudut CBA.
c. sudut C atau sudut ACB atau sudut BCA.
Jadi, ada tiga sudut yang terdapat pada Δ ABC.Dari uraian di atas dapat disimpulkan sebagai berikut :
Segitiga adalah bangun datar yang dibatasi oleh tiga buah sisi dan mempunyai tiga buah titik sudut.
B. Jenis-jenis segitiga
1. Di lihat dari panjang sisi-sisinya segitiga di bedakan menjadi tiga macam yaitu :
Segitiga sama sisi adalah segitiga yang mempunyai tiga sisi sama panjang dan semua sudutnya sama besarnya yaitu 600.
Perhatikan gambar segitiga sama sisi KLM di atas,
- Panjang KL = LM = KM
- Sudut K = Sudut M = Sudut L ( yaitu 600 )
b. Segitiga sama kaki
Segitiga sama kaki adalah segitiga dengan dua sisinya yang sama panjang dan terbentuk dari dua segitiga siku-siku yang kongruen.
Perhatikan gambar segitiga sama kaki di atas,
c. Segitiga sembarang
Segitiga sembarang adalah segitiga dengan ketiga sisinya tidak sama panjang dan juga sudut-sudutnya tidak sama besar.
Perhatikan segitiga sembarang ABC di atas ,
Segitiga yang memiliki tiga buah sudutnya berbentuk lancip dimana besar masing-masing sudutnya lebih dari 00 dan kurang dari 900 disebut dengan segtitiga lancip.
Perhatikan gambar segitiga lancip ABC di atas,
b. Segitiga siku-siku
Segitiga dengan salah satu sudutnya berukuran 900 disenut dengan segitiga siku-siku.
Perhatikan gambar segitiga siku-siku ABC di atas,
c. Segitiga tumpul
Segitiga yang salah satu sudutnya tumpul dimana salah satu sudutnya lebih dari 900 tetapi kurang dari 1800 di sebut dengan segitiga tumpul.
Perhatikan gambar segitiga tumpul PQR di atas,
3. dilihat dari panjang sisi dan sudutnya
a. Segitiga siku-siku sama kaki
Segitiga yang memiliki besar salah satu sudutnya 900 dan kedua sisinya sama panjang biasa di sebut dengan segitiga siku-siku sama kaki.
b. Segitiga lancip sama kaki
Segitiga dengan sudut lancip dan kedua sisinya sama panjang di sebut dengan segitiga lancip sama kaki.
c. Segitiga tumpul sama kaki
Segitiga yang mempunyai salah satu sudutnya tumpul dan memiliki dua sisi yang sama panjangnya.
C. Rumus untuk menghitung luas segitiga yaitu
L = ½.alas.tinggi
Sedangkan rumus keliling segitiga yaitu :
K = sisi1 + sisi2 + sisi3
Teorema Heron
Teorema ini biasanya digunakan untuk mencari luas segitiga sembarang, misal a, b dan c adalah sisi-sisinya maka
dimana
Dalam kasus segitiga sama sisi yang bersisikan a maka untuk mencari luas dan kelilingnya dapat juga menggunakan rumus sebagai berikut :
D. Dalil Phytagoras
Dalil ini hanya berlaku untuk segitiga siku – siku.

Phytagoras menyatakan bahwa c²=a²+b²
Jika terdapat tiga buah bilangan yang memenuhi pernyataan diatas maka ketiga bilangan tersebut disebut triple phytagoras.
Triple phytagoras dapat dibangun dengan menggunakan rumus diatas dengan memasukan sebuah nilai n diman n adalah bilangan bulat positif.
E. Lingkaran dalam dan luar segitiga
Lingkaran dalam segitiga merupakan suatu lingkaran yang berada didalam segitiga serta menyinggung ketiga sisi segitiga, dimana jari-jarinya dapat dicari dengan menggunakan rumus sebagai berikut

dimana :
r = jari-jari lingkaran dalamsegitiga
L= luas segitiga
s= setengah keliling segitiga
Lingkaran luar segitiga merupakan suatu lingkaran yang berada diluar segitiga dan keliling lingkaran tersebut menyinggung perpotongan tiga garis segitiga ( titik sudut ). Jari-jari lingkaran luar segitiga dapat dicari menggunakan rumus sebagai berikut

dimana :
R = jari-jari lingkatan luar segitiga
a,b,c = sisi segitiga
L = luas segitiga
Segitiga sama kaki adalah segitiga dengan dua sisinya yang sama panjang dan terbentuk dari dua segitiga siku-siku yang kongruen.
Perhatikan gambar segitiga sama kaki di atas,
- Panjang PQ = PR ( PQ dan PR di sebut kaki ).
- Sudut Q = Sudut R ( di sebut sudut-sudut kaki segitiga PQR ).
- Sisi QR merupakan alas dan Sudut P adalah sudut puncak.
c. Segitiga sembarang
Segitiga sembarang adalah segitiga dengan ketiga sisinya tidak sama panjang dan juga sudut-sudutnya tidak sama besar.
Perhatikan segitiga sembarang ABC di atas ,
- Panjang AB ≠ BC ≠ CA.
- sudut A ≠ sudut B ≠ sudut C.
2. dilihat dari besar sudutnya
a. Segitiga lancipSegitiga yang memiliki tiga buah sudutnya berbentuk lancip dimana besar masing-masing sudutnya lebih dari 00 dan kurang dari 900 disebut dengan segtitiga lancip.
Perhatikan gambar segitiga lancip ABC di atas,
- Sudut A, sudut B dan Sudut C merupakan sudut lancip.
b. Segitiga siku-siku
Segitiga dengan salah satu sudutnya berukuran 900 disenut dengan segitiga siku-siku.
Perhatikan gambar segitiga siku-siku ABC di atas,
- Sudut A merupakan sudut siku-siku yang ukurannya adalah 900.
c. Segitiga tumpul
Segitiga yang salah satu sudutnya tumpul dimana salah satu sudutnya lebih dari 900 tetapi kurang dari 1800 di sebut dengan segitiga tumpul.
Perhatikan gambar segitiga tumpul PQR di atas,
- Sudut P merupakan sudut tumpul dari segitiga tersebut.
3. dilihat dari panjang sisi dan sudutnya
a. Segitiga siku-siku sama kaki
Segitiga yang memiliki besar salah satu sudutnya 900 dan kedua sisinya sama panjang biasa di sebut dengan segitiga siku-siku sama kaki.
b. Segitiga lancip sama kaki
Segitiga dengan sudut lancip dan kedua sisinya sama panjang di sebut dengan segitiga lancip sama kaki.
c. Segitiga tumpul sama kaki
Segitiga yang mempunyai salah satu sudutnya tumpul dan memiliki dua sisi yang sama panjangnya.
C. Rumus untuk menghitung luas segitiga yaitu
L = ½.alas.tinggi
Sedangkan rumus keliling segitiga yaitu :
K = sisi1 + sisi2 + sisi3
Teorema Heron
Teorema ini biasanya digunakan untuk mencari luas segitiga sembarang, misal a, b dan c adalah sisi-sisinya maka
dimana
Dalam kasus segitiga sama sisi yang bersisikan a maka untuk mencari luas dan kelilingnya dapat juga menggunakan rumus sebagai berikut :
D. Dalil Phytagoras
Dalil ini hanya berlaku untuk segitiga siku – siku.
Phytagoras menyatakan bahwa c²=a²+b²
Jika terdapat tiga buah bilangan yang memenuhi pernyataan diatas maka ketiga bilangan tersebut disebut triple phytagoras.
Triple phytagoras dapat dibangun dengan menggunakan rumus diatas dengan memasukan sebuah nilai n diman n adalah bilangan bulat positif.
E. Lingkaran dalam dan luar segitiga
Lingkaran dalam segitiga merupakan suatu lingkaran yang berada didalam segitiga serta menyinggung ketiga sisi segitiga, dimana jari-jarinya dapat dicari dengan menggunakan rumus sebagai berikut
dimana :
r = jari-jari lingkaran dalamsegitiga
L= luas segitiga
s= setengah keliling segitiga
Lingkaran luar segitiga merupakan suatu lingkaran yang berada diluar segitiga dan keliling lingkaran tersebut menyinggung perpotongan tiga garis segitiga ( titik sudut ). Jari-jari lingkaran luar segitiga dapat dicari menggunakan rumus sebagai berikut
dimana :
R = jari-jari lingkatan luar segitiga
a,b,c = sisi segitiga
L = luas segitiga









Komentar
Posting Komentar